Dieses Kapitel soll dem interessierten Leser ermöglichen, die hier benötigten Berechnungen nachzuvollziehen und Werkzeuge in die Hand geben, selber an diesem oder an ähnlichen Problemen zu arbeiten. Die Anforderungen an Physik, Geometrie und Mathematik entsprechen in etwa Abiturniveau. Kenntnisse von Excel sind sehr hilfreich.
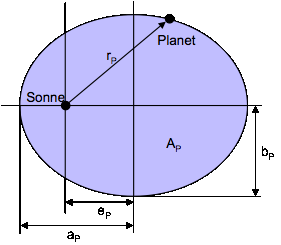
Bild 1: Geometrie eines elliptischen Orbits um die Sonne
1. Kepler-Gesetz: Planeten bewegen sich auf Ellipsen, in deren einem Brennpunkt die Sonne steht. Im Bild oben bedeuten
aP: Große Halbachse
bP: Kleine Halbachse
eP: Lineare Exzentrizität
rP: Fahrstrahl von der Sonne zum Planeten
AP: Überstrichene Ellipsenfläche bei einem kompletten Umlauf um die Sonne
Die lineare Exzentrizität errechnet sich aus den beiden Halbachsen:
![]() (1)
(1)
2. Kepler-Gesetz: Der Fahrstrahl Sonne-Planet überstreicht in gleichen Zeiten gleich große Flächen. Was heißt dies konkret?
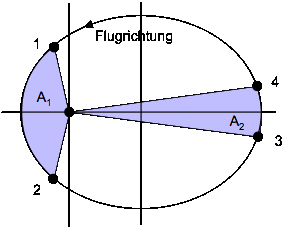
Bild 2: Das zweite Kepler-Gesetz
Beide Flächen A1 und A2 sind gleich groß. Das 2. Kepler-Gesetz besagt, dass die Zeit, die der Planet braucht, um von Punkt 1 zu Punkt 2 zu gelangen, gleich groß ist wie die Zeit von Punkt 3 zu Punkt 4. Mit anderen Worten, in Sonnennähe bewegt sich der Planet sehr viel schneller als in Sonnenferne.
3. Kepler-Gesetz: Die Quadrate der Umlaufzeiten T zweier Planeten 1 und 2 um die Sonne verhalten sich wie die dritten Potenzen der großen Halbachsen ihrer Ellipsenbahnen:
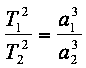 (2)
(2)
T: Benötigte Zeit für einen kompletten Umlauf um die Sonne
Was bedeutet dies? Zum einen, dass die Umlaufzeit eines Planeten um die Sonne nur von der großen Halbachse abhängt, nicht aber von der kleinen (das zweite Kepler-Gesetz ist aber zu beachten, das heißt, die Bewegung wird „unförmiger“, je kürzer die kleine Halbachse ist, weil sich im Vergleich zu einer Kreisbahn (große und kleine Halbachse gleich lang) in Sonnennähe die Geschwindigkeit erhöht und in Sonnenferne verringert).
Bei Umstellen der Formel wird zum anderen ersichtlich, dass sich für unser komplettes Sonnensystem eine Konstante ermitteln lässt, aus der sich sehr einfach die Umlaufzeit eines Planeten durch seine große Halbachse ermitteln lässt (oder durch Umstellen der Formel aus der Umlaufzeit dessen große Halbachse):
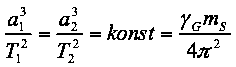 (2b)
(2b)
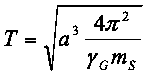 (3)
(3)
γG: Gravitationskonstante (6,672 * 10-11 m3kg-1s-2)
mS: Sonnenmasse (1,989 * 1030 kg)
Zusammengefasst hat man mit den Kepler-Gesetzen die Werkzeuge in der Hand, beliebige Umlaufbahnen um die Sonne zu bestimmen, sowohl was die Umlaufzeit als auch die Exzentrizität und die beiden Halbachsen betrifft und wie diese Größen zusammenhängen. Mehr Details lassen sich allerdings nur mit ein wenig Mathematik klären; z. B. wann der Planet wo ist (wir wissen nur, wie lange er braucht, um ein Mal um die Sonne zu kreisen) und wie schnell er sich an dieser Stelle auf seiner Bahn fortbewegt. Daher folgt zunächst eine Einführung in die Geometrie von Ellipsen.
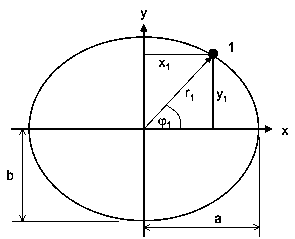
Bild 3: Charakteristika einer Ellipse
Ein Punkt 1 auf einer Ellipse kann auf mehrere Arten beschrieben werden:
Die Gleichung einer Ellipse im kartesischen Koordinatensystem (beschrieben durch die Koordinaten x und y mit dem Ursprung im Zentrum der Ellipse) lautet
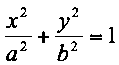 (4)
(4)
Punkt 1 muss daher ebenfalls diese Gleichung erfüllen:
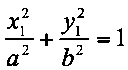 (4b)
(4b)
Mit dieser Gleichung kann aus den beiden Halbachsen bei gegebenem y oder x das entsprechende x oder y ausgerechnet werden.
Eine weitere Möglichkeit ist, den Punkt 1 über einen Winkel φ1 und einen Radius r1 zu beschreiben. Es gilt mit dem Satz von Pythagoras
![]() (5)
(5)
Außerdem folgen aus den Winkelfunktionen
![]() (6)
(6)
und
![]() (7)
(7)
Die Fläche einer Ellipse berechnet sich zu
![]() (8)
(8)
Damit sind die himmelsmechanischen und geometrischen Grundlagen vorgestellt, so dass wir zu den eigentlichen Berechnungen für diesen Artikel kommen können.
Bei Obelix lautet die Aufgabenstellung, eine elliptische Bahn so zu berechnen, dass die Umlaufzeit T genau ein Jahr beträgt und gleichzeitig die Exzentrizität so groß ist, dass die Marsbahn erreicht wird. Aus der folgenden Skizze gehen die verwendeten Größen hervor:
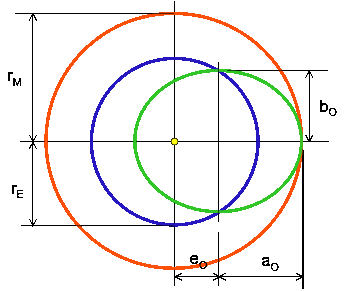
Bild 4: Zur Bestimmung der Bahndaten von Obelix
Da die Umlaufzeit von Obelix genau die gleiche wie die der Erde sein soll und die Umlaufzeit alleine durch die große Halbachse festgelegt wird, muss gelten
![]() (9)
(9)
Für die Exzentrizität folgt dann aus Bild 4
![]() (10)
(10)
Damit gilt mit Verwenden der Gleichung (1) für die kleine Halbachse von Obelix
![]() (11)
(11)
Die Radien von Mars und Erde betragen
rE = 1,49 * 1011 m
Damit ergeben sich
eO = 0,784 * 1011 m
aO = 1,49 * 1011 m
bO = 1,27 * 1011 m
Die Berechnung der Bahn von Asterix verläuft ein wenig anders. Hier ist die Ausgangsannahme, dass die Umlaufzeit um die Sonne eineinhalb Jahre betragen muss. Daraus ergibt sich mit Formel (3) als große Halbachse
aA = 1,96 * 1011 m
Zur Berechnung der Exzentrizität hilft das folgende Bild.

Bild 5: Zur Bestimmung der Bahndaten von Asterix
Es ist ersichtlich, dass gelten muss
![]() (12)
(12)
Es folgt
eA = 0,47 * 1011 m
bA = 1,90 * 1011 m
Nun sind die Bahnen der beiden Paternoster festgelegt. Es bleibt allerdings offen, wie lange die beiden auf ihren jeweiligen Reisen zwischen Mars und Erde unterwegs sind (es ist nur bekannt, dass Obelix für den kompletten Orbit ein Jahr und Asterix eineinhalb Jahre brauchen). Dieser Teil der Berechnung ist die schwierigste Aufgabe. Die Lösung des Problems erfolgt über eine numerische Näherung mit Hilfe des Tabellenkalkulationsprogramms Excel. Die Orbits von Asterix und Obelix werden mit der gleichen Methode berechnet; lediglich die Eingabegrößen sind unterschiedlich. Im Folgenden wird daher die Unterscheidung zunächst aufgehoben und nur noch von Orbits oder Ellipsen geredet.
Ansatzpunkt ist das zweite Kepler-Gesetz. Wir wissen die Zeit für einen kompletten Umlauf um die Sonne und kennen die Geometrie der Ellipse, also die beiden Halbachsen und die Fläche der Ellipse. Wir versuchen nun, die Zeit zu berechnen, die ein Paternoster braucht, um 1° an einer beliebigen Position der Ellipse zu überstreichen.
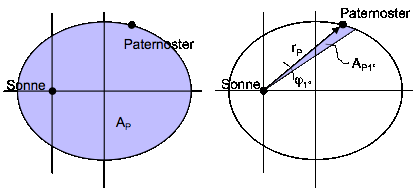
Bild 6: Zur Bestimmung der Flugzeit für einen gegebenen Winkel
Die Zeit tP1°zum Durchfliegen des Winkels φ1° kann mit folgender Formel berechnet werden, die sich aus dem zweiten Kepler-Gesetz ergibt:
TP ist bekannt, AP ist sehr leicht zu berechnen (Formel (8)). Damit ist das Problem auf die Bestimmung von AP1° reduziert. Hier hilft weiter, dass man nur einen sehr kleinen Fehler macht, wenn man die überstrichene Fläche durch ein Dreieck annähert. Das Vorgehen ist im nächsten Bild dargestellt.

Bild 7: Berechnung der vom Fahrstrahl rP(φ) überstrichenen Fläche
Die überstrichene Dreiecksfläche berechnet sich zu
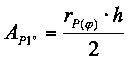 (14)
(14)
h lässt sich über Winkelgleichungen aus rP(φ+1°) berechnen:
![]() (15)
(15)
Nur am Rande soll darauf hingewiesen werden, dass man durch diese Näherung einen Teil der Fläche der Ellipse vernachlässigt, wodurch das Ergebnis nur zu einer Schätzung, nicht aber zu einem exakten Wert führt. Die Annäherung der Ellipse durch 360 kleine Dreiecksflächen zu jeweils 1° wird allerdings sehr genau und genügt den Betrachtungen in diesem Artikel. Es wird sich später zeigen, dass der Fehler bei weit unter einem Prozent liegt.
Das Problem ist nun verlagert auf die Bestimmung von rP(φ) in Abhängigkeit vom Winkel φ. Diese Berechnung ist nicht ganz einfach, obwohl wir die Geometrie der Ellipse oben bereits behandelt haben. Dort sind nämlich alle Größen auf das Zentrum der Ellipse bezogen, nicht aber auf die Sonne, die bekanntlich in Entfernung der Exzentrizität eP vom Zentrum der Ellipse liegt. Wir bezeichnen das Zentrum der Ellipse mit Z. Ein Hilfsradius r* zeigt von dort aus zu dem Paternoster. Im nächsten Bild ist der Zusammenhang des Hilfsradius mit dem tatsächlichen Fahrstrahl rPφ in Abhängigkeit des Laufwinkels φ zu sehen.
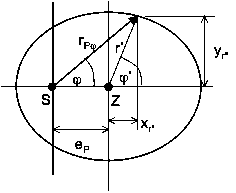
Bild 8: Bestimmung des Fahrstrahls rPj aus der Ellipsengeometrie
Aus dem Bild lassen sich einige geometrische Beziehungen ableiten. Betrachten wir zuerst die Winkelfunktionen:
![]() (16)
(16)
![]() (17)
(17)
Aus der Ellipsengleichung (Gleichung 4) folgt:
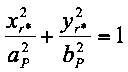 (18)
(18)
In den drei obigen Gleichungen sind drei Unbekannte: rPφ, yr* und xr*. Lediglich rPφ ist von Interesse. Es gilt also, die drei Gleichungen geeignet miteinander zu kombinieren und umzuformen, um eine einzige Gleichung für rPφ zu erhalten.
Gleichungen (16), (17) und (18) umgeformt:
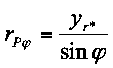 (16b)
(16b)
![]() (17b)
(17b)
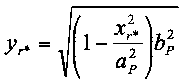 (18b)
(18b)
(18b) in (16b) liefert
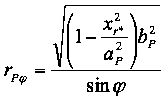 (19)
(19)
(17b) in Gleichung (19) eingebaut:
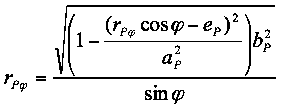 (20)
(20)
Diese Gleichung muss nun nach rPφ aufgelöst werden. Der Vollständigkeit halber hier im Detail nachvollzogen.
Zunächst werden beide Seiten der Gleichung quadriert und die Glieder bP und sinφ nach links gezogen. Außerdem wird der quadratische Ausdruck, der rPφ enthält, aufgelöst.
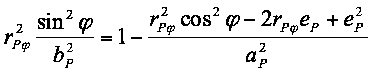 (20b)
(20b)
Die Glieder der rechten Seite der Gleichung werden nach Potenzen von rPφ sortiert.
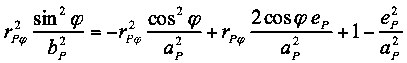 (20c)
(20c)
Die komplette rechte Seite wird nach links geholt und noch Mal nach Potenzen von rPφ geordnet.
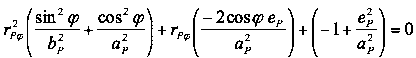 (20d)
(20d)
Zur besseren Übersicht werden die Terme in den Klammern wie folgt abgekürzt:
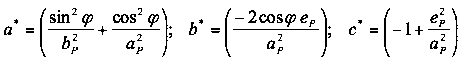
Somit ist aus (20) eine gemischt-quadratische Gleichung der folgenden Form entstanden:
![]() (20e)
(20e)
Diese Gleichung hat bekanntermaßen zwei Lösungen:
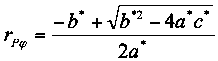 (21a)
(21a)
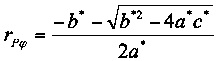 (21b)
(21b)
Von den beiden Lösungen ist nur diejenige mit positivem Wert physikalisch sinnvoll. Die andere Lösung kann ignoriert werden. Mit diesen Gleichungen lässt sich sehr einfach rPφ von φ = 0° bis φ = 360° in einer Excel-Tabelle darstellen und mit Hilfe der Formel (13) auch tP1° von φ = 0° bis φ = 360°. Durch Aufaddieren der tP1° lässt sich damit auch bestimmen, zu welcher Zeit der Paternoster welchen Winkel φ im Orbit erreicht hat; diese aufaddierte Zeit nennen wir t(φ). Die aktuelle Entfernung zur Sonne gibt rPφ an.
Mit diesen Daten kann man aber noch mehr berechnen. Von großem Interesse ist die Geschwindigkeit bei jedem Winkel φ. Diese lässt sich sehr einfach durch die beiden Strahlen rPφ und rPφ+1° sowie der Zeit tP1°(φ) = Δt(φ) berechnen.
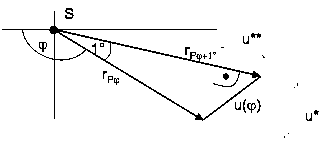
Bild 9: Bestimmung der Bahngeschwindigkeiten aus den Fahrstrahlen
Der zurückgelegte Flugweg zwischen dem Winkel φ und dem Winkel φ+1° bezeichnen wir mit u(φ). Auch hier wird wieder mit einer Näherung gearbeitet, weil in Wahrheit ja ein Bogen auf der Ellipse durchflogen wird. Die Geschwindigkeit beträgt
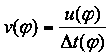 (22)
(22)
Nun gilt es, u(φ) aus den beiden rPφ zu berechnen. Dies geschieht mit den eingezeichneten Hilfsgrößen u* und u**. Mit dem Satz von Pythagoras gilt
![]() (23)
(23)
u* und u** lassen sich mit Hilfe der Winkelfunktionen errechnen.
![]() (24)
(24)
![]() (25)
(25)
Es folgt
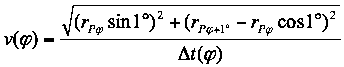 (26)
(26)
Damit ist die absolute Geschwindigkeit berechnet. Wichtiger sind allerdings die jeweiligen tangentialen und radialen Komponenten der Geschwindigkeit.
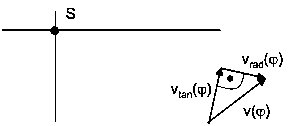
Bild 10: Vektorielle Zerlegung der Absolutgeschwindigkeiten
Es gelten hierfür:
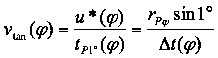 (27)
(27)
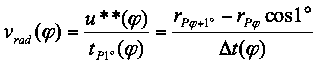 (28)
(28)
vtan(φ) und vrad(φ) sind ebenfalls in der Exceltabelle für jeden Winkel φ berechnet. Zu beachten ist, dass vrad(φ) positiv ist, wenn sich der Paternoster von der Sonne entfernt.
Die Ergebnisse für Obelix und Asterix sind in der Excel-Tabelle gezeigt.
Damit ist die elliptische Bahn der Paternoster zumindest an jedem vollen Winkel φ recht genau beschrieben.
Werfen wir nun einen genaueren Blick auf die Bahnverschiebungen. Aus der Excel-Tabelle geht hervor, dass Obelix bei seinem Flug von der Erde zum Mars die Winkel von 58° bis 360°, also 302°, überstreicht und hierfür eine Zeit von etwa 243 Tagen benötigt. Die Winkelgeschwindigkeit der Erde beträgt etwa 0,986° pro Tag. Das heißt, dass die Erde in diesen 243 Tagen 239,5° überstreicht und bei der Ankunft von Obelix am Mars diesem noch um 62,5° „hinterherfliegt“.
Gehen wir nun bei Asterix den umgekehrten Weg. Er kommt bei φ = 180° bei der Erde an und flog vorher bei φ = 38° am Mars ab (dies geht ebenfalls aus der Excel-Tabelle hervor), hat also 142° überstrichen. Gebraucht hat er dafür etwa 187 Tage, während dieser die Erde 184,3° zurückgelegt hat. Dies heißt, dass die Erde beim Abflug vom Mars 184,3° - 142° = 42,3° hinter dem Mars gewesen sein muss.
Bei der Ankunft am Mars muss die Erde also 62,5° hinter dem Mars zurück liegen, beim Abflug vom Mars noch 42,3°. Sie muss daher in der Zeit während des Aufenthalts auf dem Mars 20,2° „aufholen“. Die Winkelgeschwindigkeit des Mars beträgt 0,524° pro Tag, also holt die Erde jeden Tag 0,462° auf. Für 20,2° braucht sie etwas weniger als 44 Tage. Dies ist die Dauer des Aufenthalts auf dem Mars.
In Bild 5 in diesem Text sieht man, dass der Mars bei der Ankunft in Punkt 4 auf der horizontalen Linie liegt. Beim Abflug vom Mars hat er 0,524°/Tag mal 43,72 Tage, also 22,9°, überstrichen und Asterix überstreicht weitere 142° bis zum Erreichen der Erde, die gleichzeitig der sonnennächste Punkt, also sozusagen der Beginn des Orbits von Asterix ist. Das heißt, dass die Bahn des Asterix um 22,9° + 142° - 180° = -15,1° relativ zur Bahn von Obelix verschoben ist (im Gegenuhrzeigersinn sind die Werte positiv, was heißt, dass der Orbit von Asterix 15,1° im Uhrzeigersinn zum Orbit von Obelix gedreht ist). Der komplette Sachverhalt ist im folgenden Bild dargestellt.
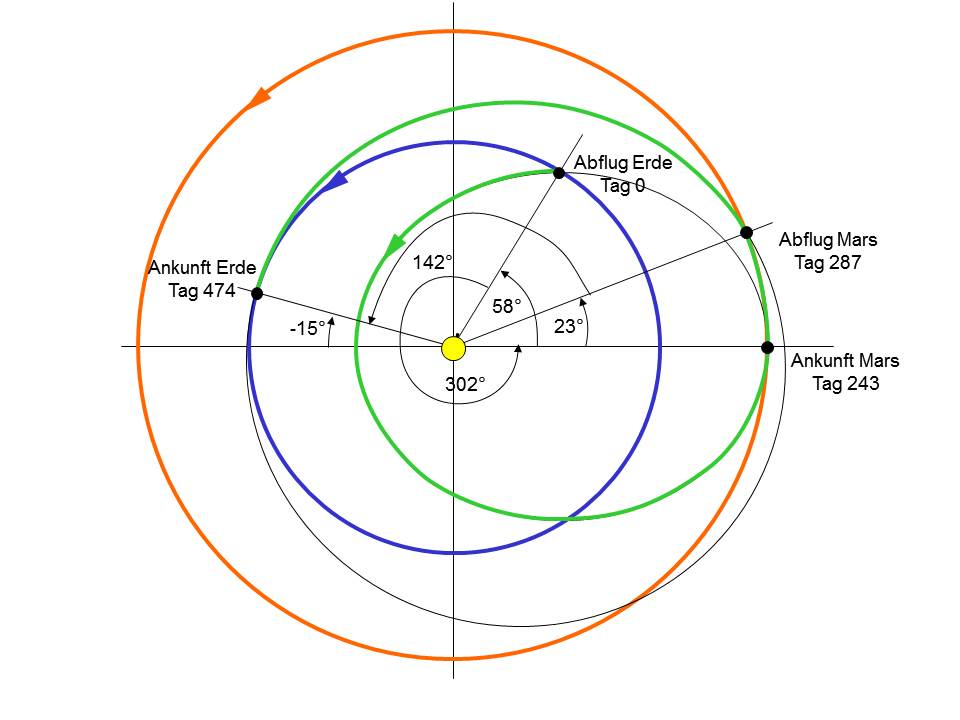
Bild 11: Geometrische Veranschaulichung der Trajektorien
Nun sollen noch die Relativgeschwindigkeiten Paternoster-Mars bzw. Paternoster-Erde berechnet werden.
Die Werte für vtan und vrad sind die Werte der Geschwindigkeitskomponenten bezogen auf das Inertialsystem. Das heißt, die jeweiligen Bahngeschwindigkeiten von Erde oder Mars müssen davon noch vektoriell abgezogen werden, um die Relativgeschwindigkeiten zu erhalten. Vereinfachend soll angenommen werden, dass sowohl Erde als auch Mars keine radialen Geschwindigkeiten haben (es wurde oben bereits angegeben, dass beide Planeten zur Vereinfachung Kreisbahnen beschreiben sollen).
Hier die jeweiligen Geschwindigkeitskomponenten für Erde und für Mars:
vtanE = 29660 m/s
vradE = 0 m/s
vtanM = 24130 m/s
vradM = 0 m/s
Beim Abflug von Obelix von der Erde muss gelten
vtanOE = 24770 m/s
vradOE = 15510 m/s
Beim Ankunft am Mars gilt
vtanOM = 16440 m/s
vradOM = 0 m/s
Diese Werte ergeben sich aus der Excel-Tabelle, wobei angemerkt werden muss, dass diese dort in der Einheit m/d, also Meter pro Tag, angegeben sind und erst umgerechnet werden müssen.
Für Asterix gilt beim Abflug vom Mars
vtanAM = 21810 m/s
vradAM = 3990 m/s
und für die Ankunft an der Erde
vtanAE = 33100 m/s
vradAE = 0 m/s
Zur Berechnung der Komponenten der Relativgeschwindigkeiten müssen nur die jeweiligen Komponenten der Erde oder des Mars abgezogen werden. Die Geschwindigkeitsbeträge resultieren dann allerdings aus den Wurzeln der Summe der Quadrate der Differenzen der beiden Geschwindigkeitskomponenten (wieder der Satz des Pythagoras). Anschaulich ist das im folgenden Bild für die Geschwindigkeit von Obelix beim Verlassen der Erde dargestellt.

Bild 12: Vektorielle Subtraktion der Absolutgeschwindigkeiten von Obelix und Erde
Es wird klar, dass gelten muss
![]() (29)
(29)
Daraus ergeben sich die bereits oben genannten Geschwindigkeitsdifferenzen:
Beim Abflug von Obelix an der Erde: ΔvOE = 16260 m/s
Bei der Ankunft von Obelix am Mars: ΔvOM = 7697 m/s
Beim Abflug von Asterix vom Mars: ΔvAM = 4621 m/s
Bei der Ankunft vom Asterix bei der Erde: ΔvAE = 3437 m/s
Es ist zu beachten, dass diese Geschwindigkeitsdifferenzen den Geschwindigkeitsdifferenzen jeweils nach Verlassen des Schwerefeldes von Erde oder Mars bedeuten. Bei der Erde sind dies also zusätzliche 3900 m/s und beim Mars 1500 m/s, wenn man sich vorstellt, dass der jeweilige „Start“ aus dem Orbit des jeweiligen Planten stattfindet. Dies sind die Differenzen der jeweiligen ersten und zweiten Astronautischen Geschwindigkeiten von Erde und Mars: Ein Körper braucht zum Erreichen einer Umlaufbahn um die Erde eine Geschwindigkeit von mindestens 7900 m/s (erste astronautische Geschwindigkeit) und zum Verlassen des Schwerefelds der Erde 11800 m/s (zweite astronautische Geschwindigkeit); beim Mars gelten 3700 m/s und 5200 m/s.
Der Mars nähert sich der Erde alle 25,7 Monate, was einem Startfenster entspricht. Grob gesprochen sind dies zwei Jahre. Sollte jedes Startfenster genutzt werden, würde ein Obelix ausreichen, sein Orbit müsste dann aber jedes Mal um exakt 51° „gedreht“ werden. Beim Verwenden des gleichen Prinzips für Asterix könnte aber nur jedes dritte Startfenster genutzt werden, also nur alle 77,1 Monate zum Mars geflogen werden. Hier wäre eine Drehung des Orbits von Asterix um 153° notwendig. Der Energieaufwand kann im Rahmen dieses Artikels nicht berechnet werden, zumal hier komplexe Swingby-Manöver an Erde, Mars und Venus genutzt werden können und sollten. Es ist aber davon auszugehen, dass es sinnvoller ist, Asterix nicht wie Obelix als „echten“ Paternoster vorzusehen sondern ihn besser nach seiner Passage am Mars bei der Erde wieder „einzufangen“, so dass er mit einem relativ geringen Energieaufwand und bereits zum folgenden Startfenster vom Erdorbit aus die nächste „Schleife“ fliegen kann. Damit wäre es möglich, mit einem Obelix und einem Asterix jedes zweite Startfenster für bemannte Marsmissionen zu nutzen, also etwa alle viereinhalb Jahre ein Mal zum Mars zu fliegen. Für die Nutzung jedes Startfensters müsste man zwei Asterixe verwenden und hätte die doppelte Startfrequenz. Ein Obelix würde jedoch genügen.
Die Idee eines Paternosters zum Mars ist nicht neu. Edwin „Buzz“ Aldrin befasst sich seit einigen Jahren mit der Möglichkeit, ein Raumschiff zwischen Erde und Mars pendeln zu lassen, das die Erde alle 25,7 Monate erreicht und dann nach einer Flugzeit von 146 Tagen am Mars vorbei fliegt. Die Vorbeiflüge an der Erde müssen genutzt werden, um durch ein Swingby-Manöver den Orbit um 51° zu drehen. Für den Rückflug zur Erde muss ein weiterer Paternoster installiert werden. Beim Flug Erde-Mars legt das Raumschiff um die Sonne 133° zurück, die Erde aber ungefähr 144°. Sie ist bei der Ankunft am Mars dem Raumschiff (und Mars) 11° voraus. Dies bedeutet, dass die Astronauten für den Rückflug auf dem Mars warten müssen, bis die Erde wieder 11° hinter dem Mars ist, was erst nach 732 Tagen der Fall ist. Das Aldrin-Konzept ist also nicht für Kurzzeitmissionen wie die hier beschriebene geeignet. Der massebezogene Energieaufwand ist darüber hinaus deutlich höher als bei einer Hohmann-Typ-Mission. Die Vorteile des Aldrin-Paternosters würden erst bei einer Besiedelung des Mars mit vielen regelmäßigen Flügen zum Tragen kommen.